When the turbo generator is at the neutral end of the two ends, the stator is short-circuited. When the rotor rotates at synchronous speed and X;=X丨, the stator phase current is a time-frequency sinusoidal function.
Applying the symmetrical component method, the positive sequence (P), negative sequence (N) and zero sequence () components of the stator current are as follows: If the stator current is considered to be concentrated on the inner circumference of the stator core and along the axial direction of the motor (Z direction) The flowing unidirectional current sheet, the three-phase composite line density of each sequence current on the chip can be extended to the Fourier series along the circumferential coordinate, wherein the positive sequence current synthesizes the dense spatial fundamental wave component Zap (referred to as P wave), negative Sequence current synthesis of dense spatial fundamental component and ZaN (abbreviated as N wave) and zero sequence current synthesis of dense spatial 3rd harmonic forward wave component (referred to as /wave) and reverse wave component and Zaft (referred to as 6 wave The general expression of the table is the harmonic order of the table space: v=1 represents the space fundamental wave (P, N), v=3 represents the space 3rd harmonic (/, b); Kan and jan represent the phase guard 3+ A2 dragon 'quantity and amplitude and initial phase angle: the household wave is a forward traveling wave that rotates at the synchronous speed with the rotor, and no induced current is generated in the rotor. And the 6-wave is the reverse traveling wave of the reverse steering rotation, and the /-wave is the forward traveling wave which is steered and rotates at the synchronous speed of 1/3, and generates an induced current in the solid rotor.
The negative sequence current wave may generate a strong current in the solid rotor, causing local overheating of the rotor, which may cause damage to the motor in severe cases. From the safety point of view, the size of the negative sequence current must be limited, as the negative sequence capability of one of the important technical indicators of the motor is set for this purpose. As for the zero-sequence current, the traditional motor theory believes that due to the large air gap of the motor, the zero-sequence current has three weak (and multiple times three) harmonic magnetic fields, and the current generated in the rotor circuit is very small, which can be ignored. . This is debatable. Through the network analysis of the transient process, the author finds that the zero-sequence current space 3rd harmonic flux can generate significant current in the rotor core when the two-phase or single-point mid-point short circuit occurs in the turbo generator. In this paper, the electromagnetic field analysis method is used to compare the currents generated by the stator negative sequence and zero sequence current in the solid rotor of the turbo generator in the short-state steady state of the two relative midpoints, and the same results as the network analysis are obtained.
2 Two relative midpoint short-circuit steady state rotor core current and air gap magnetic field 2.1 calculation model and the basic equation solution as a fundamental study of this proposition, this paper uses a general simplified model for analysis, the basic assumption is: assume motor infinity Long, the stator current has only an axial (z-direction) component, thereby simplifying the motor electromagnetic field into a two-dimensional parallel plane field.
It is assumed that the stator core is a superconducting magnet, and its magnetic permeability is "Â¥, conductivity a0; the rotor core is "const, aconst." The whole motor is a magnetic linear medium, and the superposition principle is applied.
Falsely, the rotor core is smooth and has no slots, and the rotor field winding is open (the result is accurate for the shaft). The stator current is a unidirectional (z-direction) current piece concentrated on the circular cylindrical surface of the stator core, and the linear density space fundamental wave 0V wave of the negative sequence current and the zero-density current line density forward and reverse space 3 Subharmonics/waves and 6 waves) are excitation sources.
To further simplify the analysis, the surface of the stator core is flattened by ignoring the curvature of the stator core, and can be analyzed in a Cartesian coordinate system, thus obtaining a physical model for field analysis as shown. In Figures 1, 2 and 3, domain 1 does not have to be considered, and only domain 2 and domain 3 have to be analyzed.
Medium (x, j, z) is a stator rectangular coordinate system with a zero line (x = 0) of the axis A of the A phase, and (x', >>, z) is zero with the d axis of the rotor as the coordinate x' Rotor Cartesian coordinate system of line (x'0).
The expression of the initial phase angle v and the angular frequency A of the stator line electric dense wave phasor KZav in the rotor rectangular coordinate system (x', j, z): using the vector magnetic position J as a description function, because the system is parallel In the plane field, J has only the axial component. In the case of ignoring the displacement current, 4 satisfies the Laplace equation and the diffusion equation in domain 2 and domain 3 respectively: using the sinusoidal traveling wave electromagnetic field and the similarity of za in the coordinate x (x and time change law) Substituting equations (7) and (8), and using the following boundary conditions to obtain the penetration depth.
Substituting equation (14) into equation (13), the approximate expression yv of Krv is related to the m and s of the rotor medium and the class (n, /6) of the stator plane current linear density traveling wave. In the case of the same m and s, yvsyjsyy, and both are less than 3/4, the curves 1', 2', and 3' in the example represent ¥, */, and ¥6 of the motor of the example, respectively, and the saturation of the core is high. (m/m.<100), yN=3/4, jRN finds jaN-Rn approximation and inverse phase.
The instantaneous value lRv of the rotor induced current is determined by substituting jRv in equation (6) and jRv in equation (18) into the above equation, and obtaining the expression r-Irnsin of Irv under different initial conditions (/0). (2w/ =0 or the current induced by the stator zero-sequence current in the rotor is equal to the sum of lRf and lRb: since Dyf is very close to Dyb, approximately Dyf=D*=D*, the maximum value of 1R0 is 1R0max: A little analysis of equation (21) shows that *max is at time t=left 6/W0 (left=0, this distance t/3 (equal to space 3 harmonic pole distance t3). Since Dy is small, (soil t/ 2-tDy/36)=*t/2, indicating that lR0max is approximately periodically repeated at the axis and at a distance t/3 from it.
The zero-sequence induced current maximum value lR0max and the negative-sequence induced current are the most integrated from y=S to y=*, and the ratio of the current large value iRNmax=IrN in the unit tangential length of the rotor surface is: - rotor damping zero basis The current is substituted into the above formula for the relevant quantities of equations (2) and (4). The above data should be substituted into the relevant formula and pressed according to; u/Chan = 30, 50, 500 for ', ', 4 and /R (0) /1) The calculation is performed, and the calculation results are shown by curves 1, 2, 3, and 4, respectively. Curve 4 shows that under the short circuit condition discussed, the current induced by the zero sequence current in the solid rotor is much larger than the induced current of the negative sequence current. In view of the high degree of rotor saturation, it is advisable to take it; / = 50100, corresponding to (0/1) leg = 2.092~2.002. This result is obtained by applying network analysis under the same short-circuit condition ((1\ and 7) Yuan 3\ is the rotor, the maximum current induced by the negative sequence current and the zero sequence current on the shaft, which can be mutually supported.
It decreases as the "increases", which is the inevitable result of the decrease in the penetration depth Av and the increase in the electrical impedance due to the increase in V.
Sub-N wave induced current iRN (curve 1, chain line, drawn according to py0=0), f- and b-wave composite induced current iR0 (curve 2, dashed line) and rotor synthetic induced current line 3, solid line) The distribution of the tangential direction of the rotor (x' direction). Approximate AyN =0. It can be seen that after the zero-sequence current is measured in the rotor's induced current iR0, the actual induced current iR of the rotor significantly exceeds the induced current iRN of the stator negative-sequence current in most parts of the rotor, especially In the vicinity of the q-axis (and the distance t/3), the above equation is compared with the equation (17) to obtain an important relationship. This equation shows that for the field outside the rotor, the induced current in the rotor can be used for current sheets on the surface of the rotor. The surface current density is exactly equal to 1 rv, and the equivalent rotor can be regarded as a superconducting magnet with Z=* and c=0.
Whether the rotor has an induced current pair 1 = 0 has no effect on '2+=.+). If the rotor is a superconducting magnet with c=0 and Z=¥, Bx2v(y=0+)(Hx2v(y=0+)) remains unchanged, and Bx2v(y=8-)(Hx2v(y=8) -)) is reduced to 0, the magnetic induction of the rotor surface has only the normal component, and both By2v(y=.) and By2v(y=d) are larger than when it is a finite value. As a general rule, the increase of Z leads to the air gap. The tangential magnetic induction intensity decreases and the normal magnetic induction intensity increases. As evidence, the example data and related formulas are used to calculate the rotor induced current (when c0) is absent (at this time c=0) and different z/z0 The value of the magnetic induction of the rotor surface, and the calculation results are shown in the form of curves (the tangential magnetic induction of the rotor surface: curves 1 and 2 respectively represent the rotor no induced current, ie 1 and 2 respectively represent the rotor non-inductive current (a = 0 When 3, 4, and 5 respectively represent the rotor with induced current (a0), the sub-cores are superconducting magnets, and the rotor core has no induced current), the ratio is called the coupling coefficient, and is represented by a symbol: curve; curve 3, 4, and 5 respectively represent the rotor with an induced current of 52 rushes I), 2/(-), and soul jin) and It can be seen that with the increase of u/rt, the tangential Bb 衾 magnetic induction intensity decreases, and the normal magnetic induction intensity increases.
The size of this has a big impact on this ratio. The magnitude of the flux of each wave and thus the magnitude of the induced current in the rotor is mainly determined by the magnitude of the stator negative sequence current and the zero sequence current itself. In this case, the zero sequence current is much larger than the negative sequence current (total 0/=2.5). It is a matter of course that the rotor induces a current greater than the latter.
3 Conclusions (1) The coupling coefficient between the fundamental wave circuit of the fixed and rotor (iron core) of the turbo generator and the coupling coefficient between the third harmonic circuits are very different. The air gap blocking space 3rd harmonic flux cannot be established. .
(3) At the two relative midpoints, the short-circuit steady state, the zero-sequence current is much larger than the negative-sequence current, and the current induced in the rotor core is much larger than the induced current of the negative-sequence current. Therefore, in determining the steady-state negative sequence capability/2, the effect of the zero-sequence current should also be considered.
Acknowledgements I would like to express my heartfelt gratitude to the Kong Li researcher who gave care and support.
1. Description of GH sand and gravel pump
Naipu G series Gravel and sand slurry pump is
designed specifically for continuous pumping of extremely aggressive
slurries, with a wide particle size distribution. Capable of handling
large particles at consistently high efficiencies results in low cost of
ownership. The large volume internal profile of the casing reduces
associated velocities further increasing component life.
Typical Applications---
Slag Granulation
Suction Hopper Dredging
Dredging
Barge Loading
Sand Reclamation
Sugar Beet
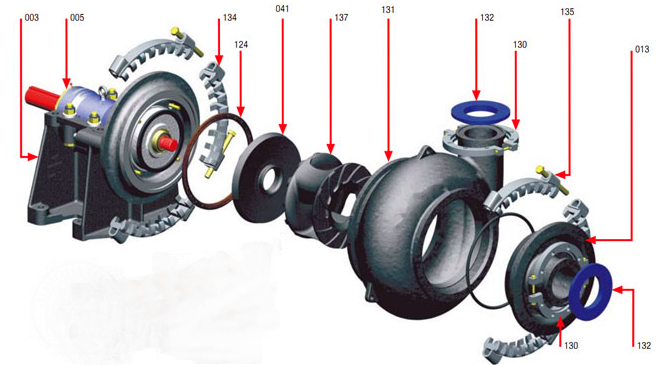
2. Construction drawing for Naipu GH sand and gravel pump
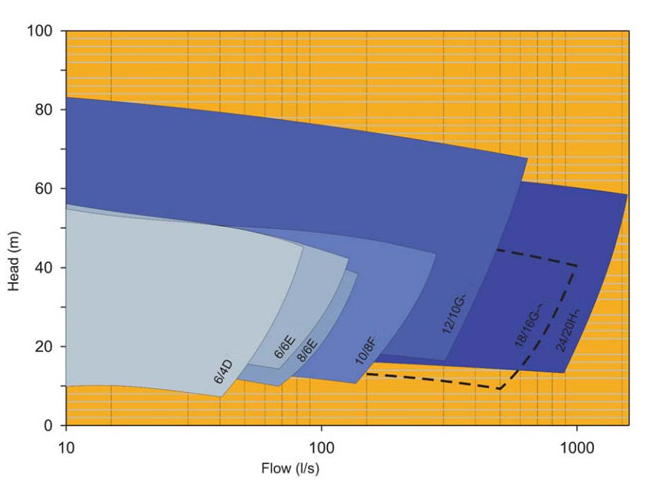
3. Select chart of GH sand and gravel pump
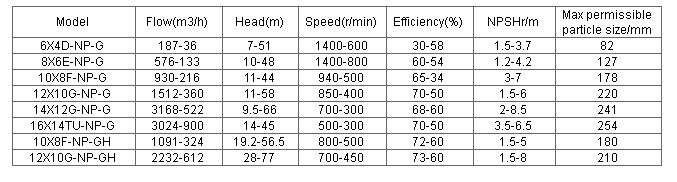
4.Performance parameters of GH sand and gravel pumps
Gravel Pump, Sand Pump,High Head Gravel Pump,GH Gravel Pump,Dredging Pump,Sand Gravel Pump
Shijiazhuang Naipu Pump Co., Ltd. , https://www.naipu-pump.com